시작하기 전에…

 

안녕하세요 공대생의 오아시스입니다. ^^

이번 시간에 배울 내용은 테브난, 노턴 등가회로 (Thevenin, Norton Equivalent Circuit) 인데요.

개념 자체는 쉽지만 문제 해결 과정이 어렵다보니 많은 분들이 어려워하시는 단원 중 하나입니다.

차라리 어렵기만 하면 다행인데 틈만 나면 나오는 녀석이라 공부를 안할 수도 없는 노릇이죠 ㅜㅜ

아무튼 잘 전달될지는 모르겠지만 제가 이해했던 과정을 이 글에 그대로 담아볼테니 잘 따라와주세요…!

 

 

1. 등가회로 (Equivalent Circuit)

 

테브난, 노턴 등가회로를 배우기 위해서는 우선 등가회로(Equivalent Circuit)가 무엇인지 부터 알아야합니다.

다음과 같이 내부를 들여다볼 수 없는 박스(점선)안에 임의의 복잡한 회로를 두고 부하저항 \mathrm{R_L}을 연결한 상황을 생각해봅시다.

 

 

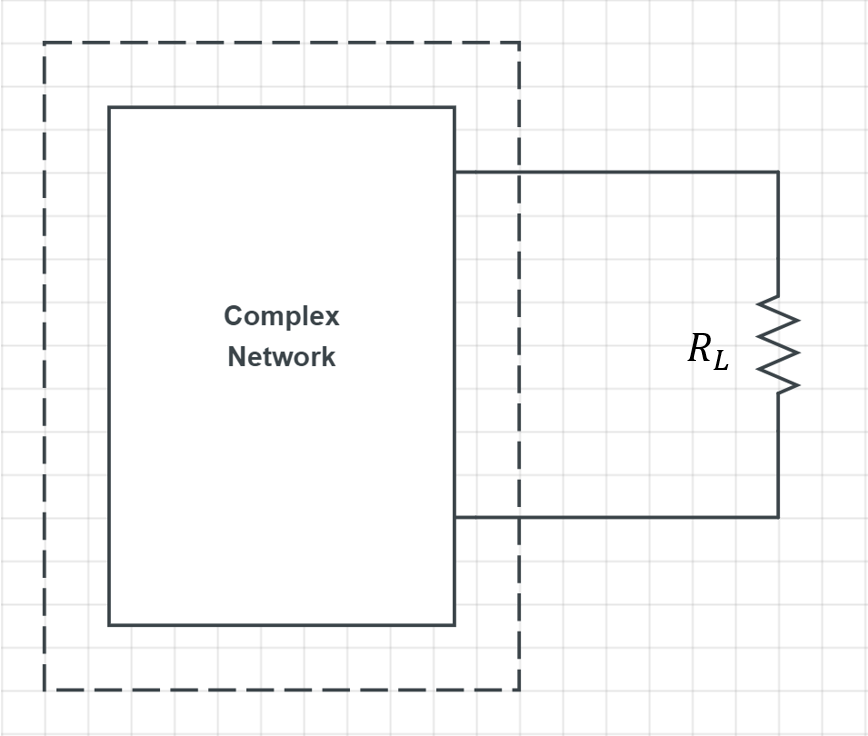
이때 박스 안의 복잡한 회로가 다른 모양의 회로로 바뀐다고 해도 부하저항에 주는 전류, 전압이 완전히 같다면 출력만 봐서는 박스 안의 회로가 달라졌는지 아닌지 구분할 수 없을 것입니다.

 

 

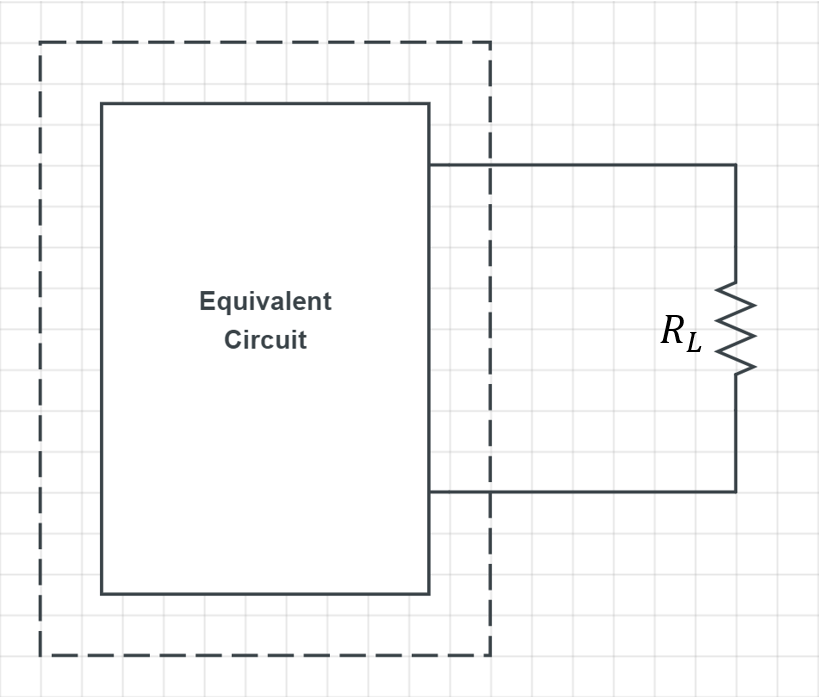
이런식으로 기존 회로와 바꿔치기해도 내부를 들여다보지 않는 이상 차이를 알 수 없는 회로를 등가회로(Equivalent Circuit)라고 합니다.

 

 

2. 테브난, 노턴 등가회로 (Thevenin, Norton Equivalent Circuit)

 

테브난, 노턴 등가회로는 이러한 등가회로 중에서도 특별한 형태를 가지는 등가회로를 말합니다.

 

 

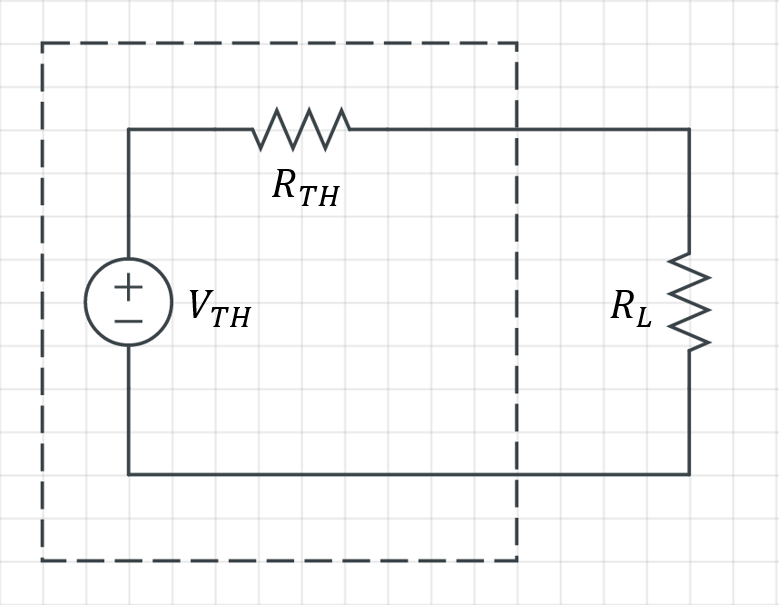
테브난 등가회로(Thevenin Equivalent Circuit)

 

테브난 등가전압원 \mathrm{V_{TH}}와 테브난 등가저항 \mathrm{R_{TH}}의 직렬 구성으로 이루어진 등가회로입니다.

 

 

 

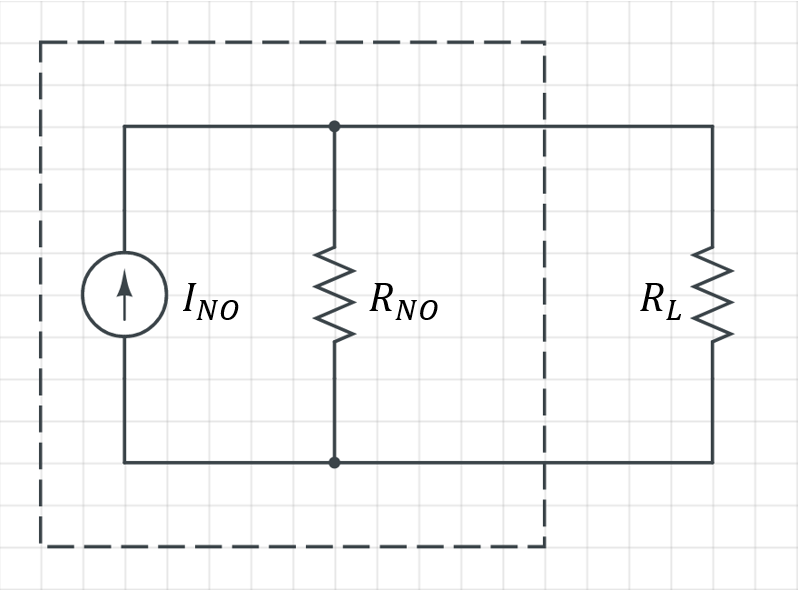
노턴 등가회로(Norton Equivalent Circuit)

 

노턴 등가전류원 \mathrm{I_{NO}}와 노턴 등가저항 \mathrm{R_{NO}}의 병렬 구성으로 이루어진 등가회로입니다.

 

 

이때 테브난, 노턴 등가회로 사이에는 특별한 관계가 존재하는데요.

이 관계를 이용하면 테브난 → 노턴, 혹은 노턴 → 테브난으로의 변환이 손쉽게 가능합니다.

 

\mathrm{V_{TH}=I_{NO}R_{TH(NO)}}

 

관계를 외우는 것은 크게 어렵지 않습니다. 그냥 옴의 법칙 형태만 생각해주면 되니까요.

 

간단한 예를 통해 실제로 이 관계가 어떻게 이용되는지 알아보죠.

아래 회로의 노턴 등가회로를 구해보겠습니다.

 

 

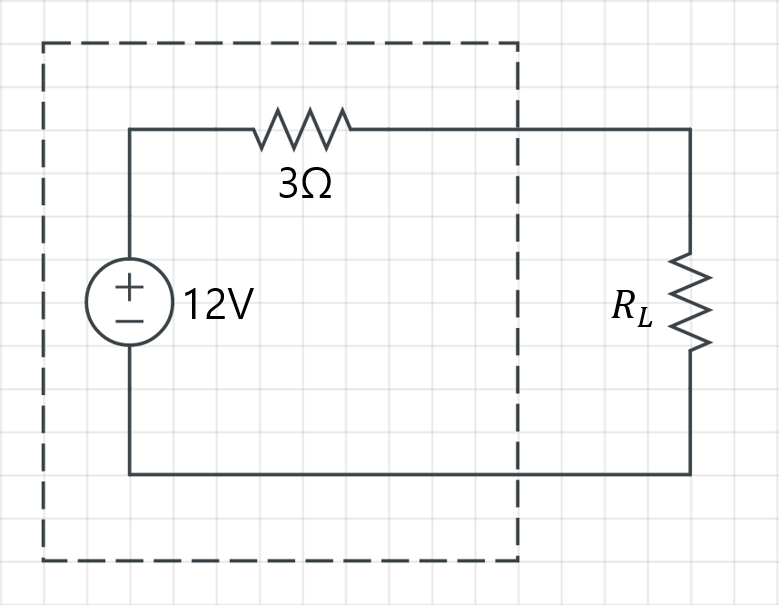
박스 안의 회로는 전압원과 저항의 직렬 구성으로 이루어져있으므로 테브난 등가회로 형태입니다.

따라서 \mathrm{V_{TH}=I_{NO}R_{TH}}을 이용하면 노턴 등가전류원의 전류값은 \mathrm{I_{NO}=12/3=4A}임을 알 수 있습니다.

 

다음은 노턴 등가저항인데 테브난, 노턴 회로가 서로 등가회로 관계에 놓였을 때 \mathrm{R_{TH}=R_{NO}}가 성립함을 이용합니다.

즉 노턴 등가저항의 저항값은 테브난 등가저항의 저항값을 그대로 가져오시면 됩니다. 간단하죠? ^^

(이러한 특징 때문에 노턴 등가저항을 따로 구분하지 않고 \mathrm{R_{TH}}로 표시할 때가 종종 있습니다.)

 

 

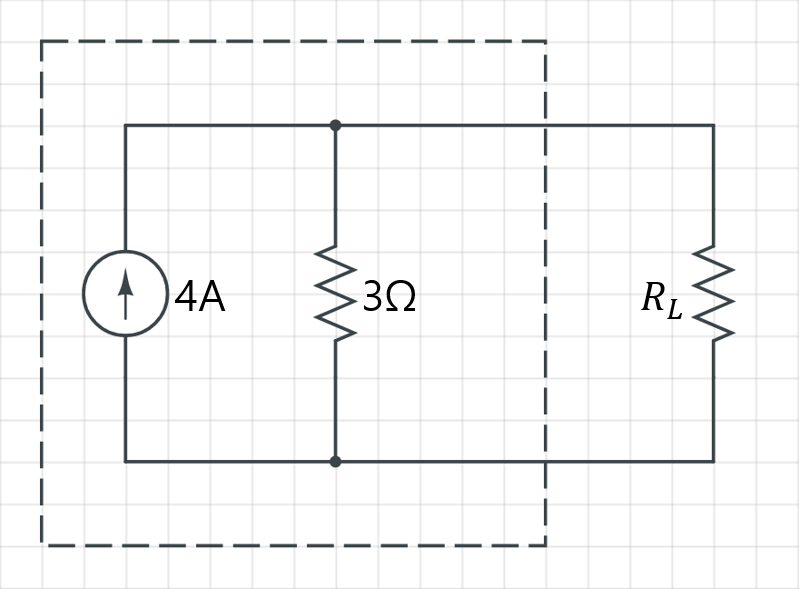
위에서 구한 값들을 이용하여 박스 안의 회로를 노턴 등가회로로 변환해준 모습입니다.

이러한 관계 덕분에 테브난, 노턴 등가회로 둘 중 하나만 구하면 나머지 하나는 거저 구할 수 있으며, 이 과정을 전원 변환(Source Transformation)이라고 부르기도 합니다.

 

 

3. 테브난 등가회로(Thevenin Equivalent Circuit) 구하기

 

자 이제 본론인 테브난 등가회로를 구하는 방법에 대해 설명드리려고 합니다.

앞서 말씀드렸듯이 노턴 등가회로는 테브난 등가회로를 구하면 간단히 구할 수 있으므로 여기서는 테브난 등가회로만 다룰 예정입니다.

 

 

우선 테브난, 노턴의 정리에 의해 모든 선형회로(우리가 흔히 알고 있는 전원, 저항, 커패시터, 인덕터로 이루어진 회로)는 테브난, 노턴 등가회로로 변환될 수 있습니다.

말이 어려웠나요? 그냥 ‘웬만한 회로는 다 테브난, 노턴 등가회로로 변환 가능하구나~’ 라고 생각하시면 됩니다.

보통 이 정리를 의식하면서 등가회로를 구하지는 않지만 그래도 이유는 알아두는 것이 좋을 것 같아 가져와봤습니다. ^^

 

아무튼 이렇게 변환 가능 여부도 확인했으니 본격적으로 변환 과정을 파헤쳐봅시다.

글로만 서술하기에는 추상적인 내용이 많으므로 간단한 예시와 함께 진행하도록 하겠습니다.

 

 

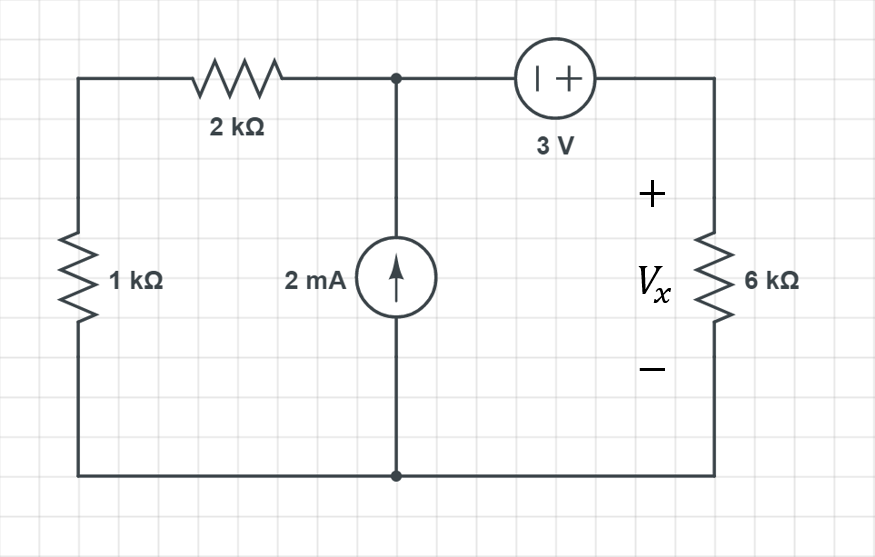
위와 같이 6kΩ 저항에 걸리는 전압 \mathrm{V_{x}}를 구하려고 하는데 연결된 회로가 복잡한 탓에 쉽게 구할 수가 없는 상황을 가정해봅시다.

이때 연결된 회로를 좀 더 단순한 형태로 변환해줄 수 있다면 간단히 전압을 구할 수 있겠죠?

바로 이러한 욕구가 생길 때 테브난, 노턴 등가회로 변환을 이용합니다.

(물론 노드 해석법, 메쉬 해석법을 이용해도 전압을 구할 수 있겠지만 배우는 차원에서 테브난 등가회로를 한번 이용해보자구요. ^^)

 

 

Step 1. 블랙박스 영역 지정과 부하측 분리

 

회로의 테브난 등가회로를 구하기 위해 가장 먼저 해야할 일은 ‘블랙박스 영역 지정’ 과 ‘부하측(Load) 분리’입니다.

말이 좀 어려웠나요? ^^ 쉽게 말해서 전체 회로 중에서 변환할 범위를 선택해주고 분리시켜주면 됩니다.

 

 

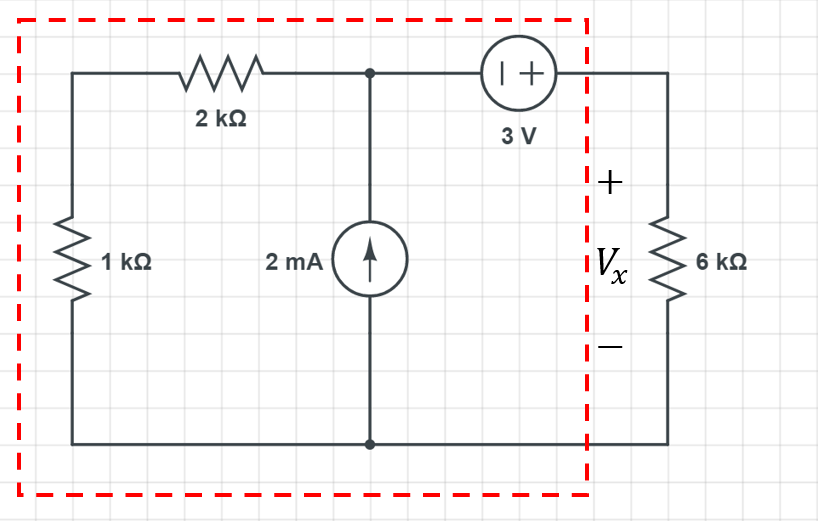
이렇게 좀 더 간단해지길 원하는 부분을 선택해주고…

 

 

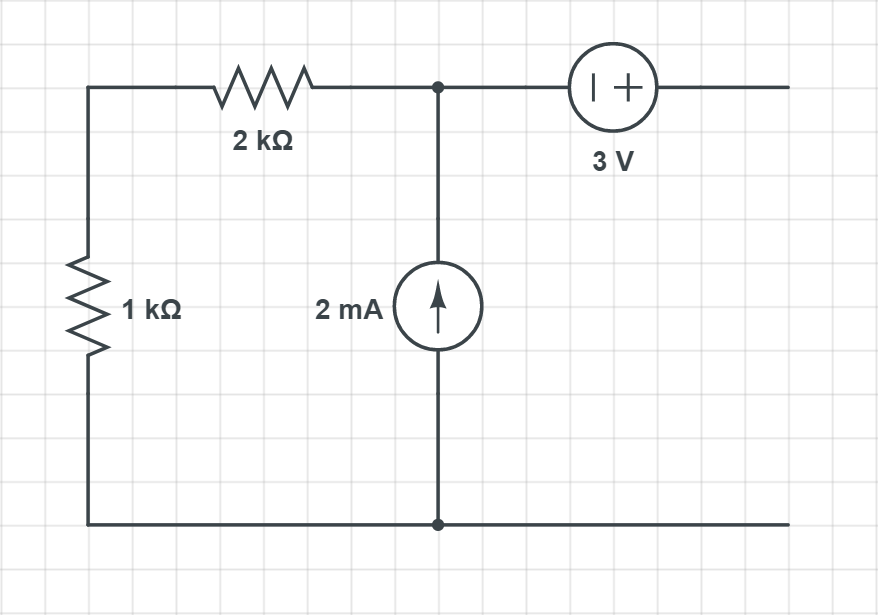
그 부분의 영향을 받는 부하측을 위 그림처럼 톡 떼주면 됩니다.

어때요, 간단하죠? ^^

 

 

Step 2. 등가전압원의 전압값 \mathrm{V_{TH}} 구하기

 

 

자 이제 테브난 등가회로로 만들어줄 회로도 정해졌으니 테브난 등가회로가 어떻게 생긴 녀석이었는지 한번 생각해봅시다.

그림을 보니 테브난 등가회로를 그리기 위해서 구해야하는 것은 두 가지인데요,

등가전압원의 전압값 \mathrm{V_{TH}}와 등가저항의 저항값 \mathrm{R_{TH}}입니다.

 

우선 등가전압원의 전압값 \mathrm{V_{TH}} 부터 구해볼까요? ^^

결론부터 말씀드리자면 \mathrm{V_{TH}}는 변환 대상으로 선택한 회로의 Open(개방)부분에 걸리는 전압 \mathrm{V_{o}}와 같은 크기를 가집니다.

 

 

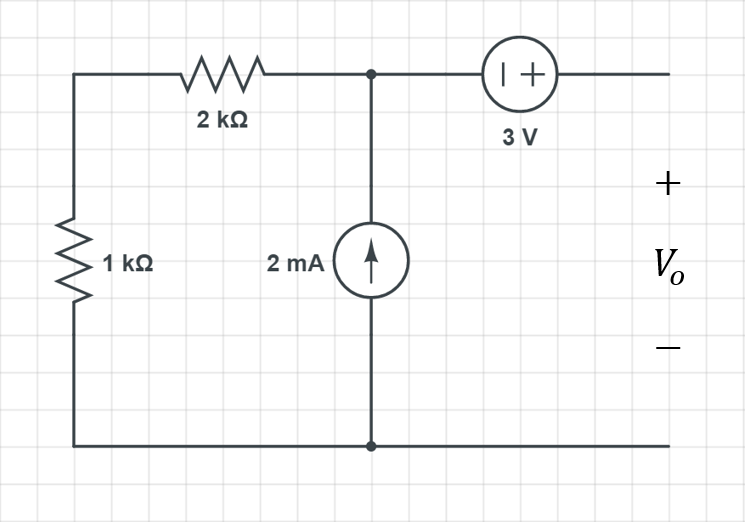
이때 중요한 것은 이 \mathrm{V_{o}}는 원래 상태에서의 전압 \mathrm{V_{x}}와 같은 값을 가지지 않는다는 것인데요.

 

 

\mathrm{V_o \neq V_x}

 

부하가 연결되면 기존 회로의 전체적인 전류 흐름과 전압 분배에 변동이 생기기 때문입니다.

처음 배울 때 많이들 헷갈려하시는 부분이니 꼭 제대로 알고 넘어가시기 바랍니다.

 

 

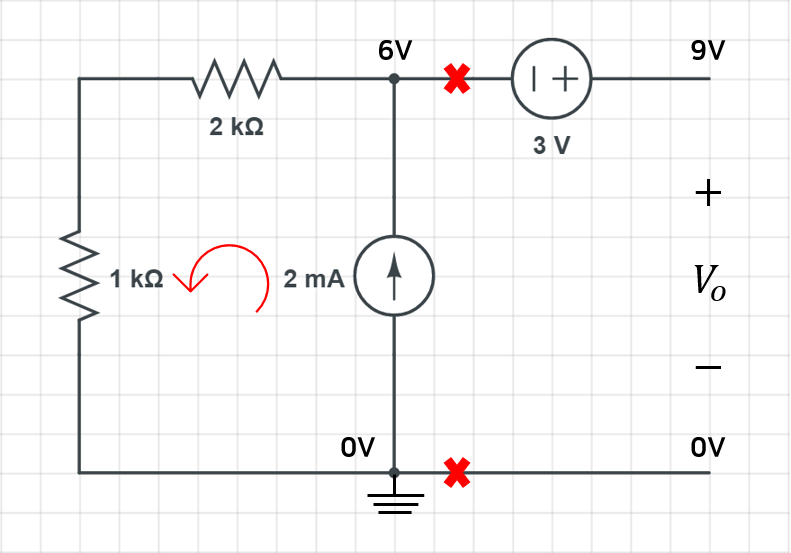
아무튼 다시 돌아와서 \mathrm{V_{o}}를 구해봅시다.

전류가 흐르는 것은 왼쪽 부분 뿐이고, 오른쪽 부분은 끊어져있으므로 전류가 흐르지 않습니다.

이 점에 유의하여 KVL과 노드 해석법을 이용하면 \mathrm{V_{o}}은 9V라는 것을 쉽게 알 수 있고, 이것이 곧 등가전압원의 전압값, \mathrm{V_{o}}가 됩니다.

간단한 과정이므로 자세한 설명은 생략하였는데, 혹시 이해가 되지 않으신다면 KVL, 노드 해석법에 대한 강의를 참고하시기 바랍니다.

(KVL 강의 링크 / 노드 해석법 강의 링크)

 

회로의 Open(개방) 전압 \mathrm{V_{o}}가 테브난 등가전압 \mathrm{V_{TH}}가 되는 이유는 아래와 같습니다.

 

 

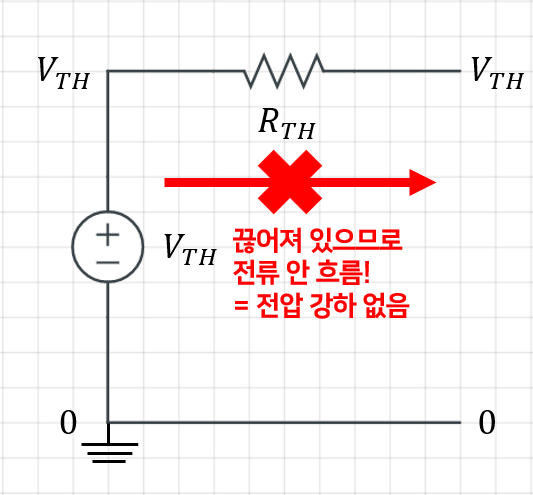
부하를 분리시켜놓은 회로를 테브난 등가회로로 변환시키면 마찬가지로 부하가 분리된 Open(개방) 회로가 나옵니다.

이때 끊어진 상태의 회로에서는 전류가 흐르지 않기 때문에 저항을 지나도 전압 강하가 일어나지 않고, 결국 테브난 등가회로의 양 끝에는 \mathrm{V_{TH}}의 전압이 그대로 걸리게 되는데요.

이름이 ‘등가전압’인 만큼, 부하를 연결하지 않은 상태의 전압 \mathrm{V_{o}}와 동일한 전압을 공급해주어야 하기 때문에 \mathrm{V_{o}=V_{TH}} 관계가 성립합니다.

 

처음엔 이해가 잘 안돼도 괜찮습니다. 어차피 배우다보면 깨닫는 날이 오니까요. ^^

이해가 안된다면 너무 조급해하지 마시고 일단 ‘그냥 그런가보다~’ 하고 넘어가시기 바랍니다. ㅎㅎ

 

 

Step 3. 등가저항의 저항값 \mathrm{R_{TH}} 구하기

 

 

테브난 등가전압원의 전압값 \mathrm{V_{TH}}를 구했으니 이제 남은 것은 테브난 등가저항의 저항값  \mathrm{R_{TH}}입니다.

복잡하게 얽혀있는 저항들을 어떻게 하나로 만드느냐… 인데 의외로 간단합니다.

 

 

우선 아까 그 회로에서 ‘중첩의 원리’를 적용하듯이 전압원은 Short(단락) 전류원은 Open(개방) 상태로 만들어주어야 합니다.

 

 

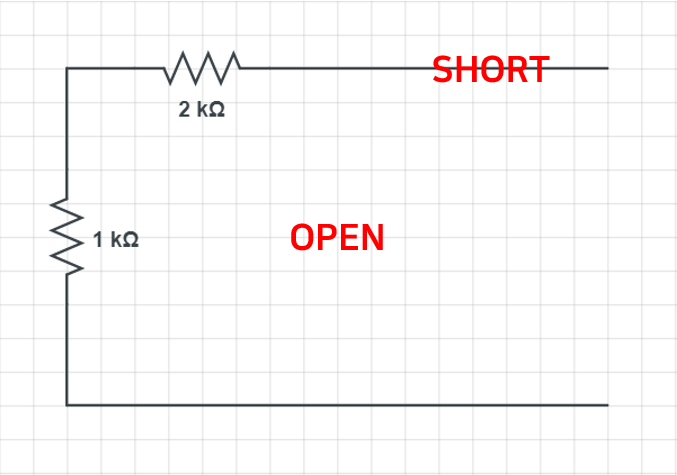
과정을 거치면 회로에는 위처럼 저항만 남는데요.

이때 분리된 부하의 자리를 기준으로 합성저항을 구해주면 그게 바로 테브난 등가저항입니다.

 

 

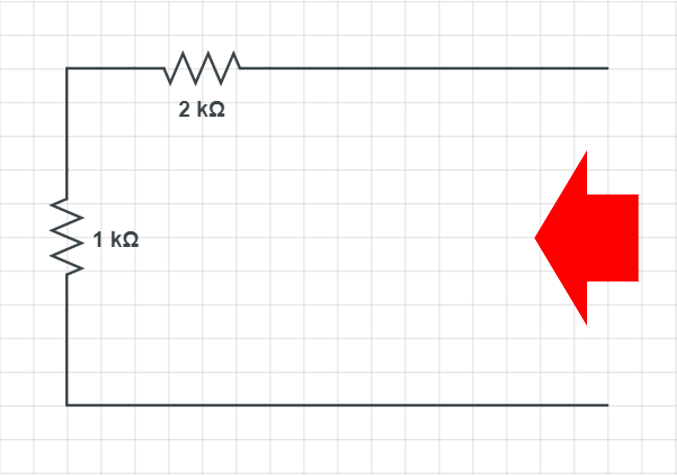
말이 좀 어렵죠?

그냥 뚫린 자리에 전원이 있다고 생각하고 평소 합성저항 구하듯이 하시면 됩니다.

이 경우 저항 두 개가 직렬로 연결되어있으니까 1kΩ + 2kΩ = 3kΩ 이 되겠네요.

(지금 보여드린 예시는 간단하지만 실제로는 까다로운 상황들이 많습니다. 많은 연습만이 살 길!)

결론적으로 테브난 등가저항 \mathrm{R_{TH}}는 3kΩ 이 되는겁니다.

 

사실 이유를 좀 더 자세히 설명드리고 싶었지만… 추상적인 내용이라 글이 너무 길어질 것 같아서 생략했습니다.

여기서는 일단 중첩의 원리를 응용한 과정이라는 것 정도만 알아두시기 바랍니다.

 

 

Step 4. 테브난 등가회로 그리기

 

 

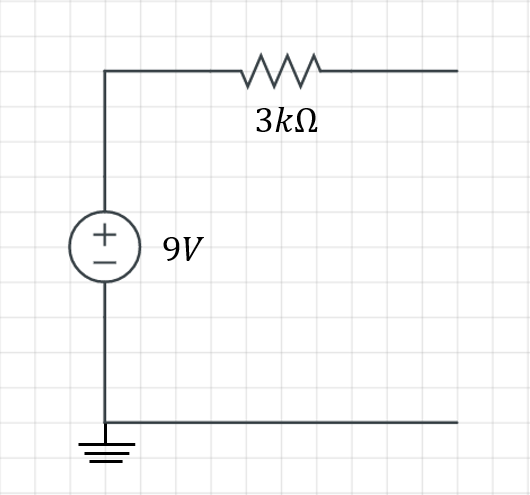
이제 어려운 부분은 다 끝났습니다.

구해놓은 \mathrm{V_{TH}}, \mathrm{R_{TH}} 값을 이용하여 위와 같이 테브난 등가회로를 그려줍니다.

이때 회로에는 아직 전류가 흐르지 않으므로 양 끝단에 9V 전압( \mathrm{V_{TH}=V_o} )이 그대로 걸리게 된다는 사실을 기억해두시기 바랍니다.

 

테브난 등가회로도 구했으니 부하측을 다시 연결해볼까요?

우리의 원래 목적은 6kΩ 저항에 걸리는 전압 \mathrm{V_{x}}를 구하는 것이었으니까요. ^^

 

 

 

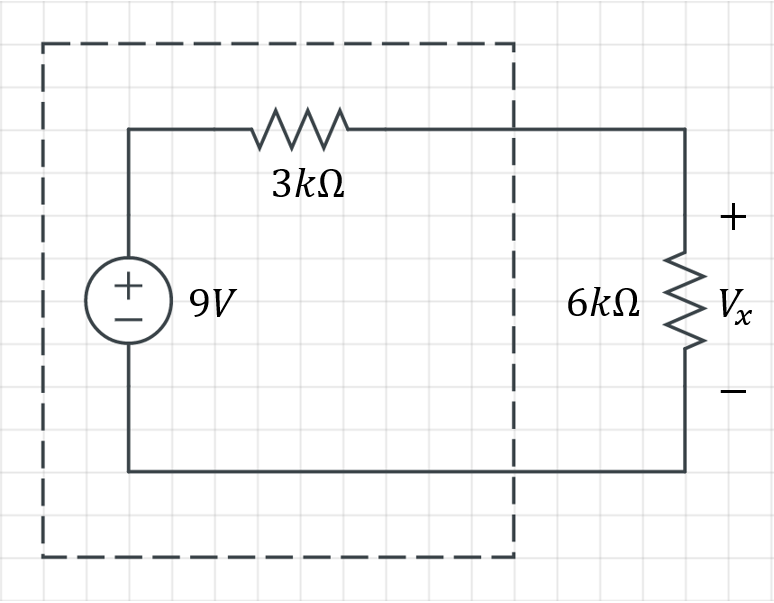
그림과 같이 변환 전 회로가 있던 자리에 테브난 등가회로를 대신 끼워넣어주면 됩니다.

어때요? 전압 구하기가 훨씬 쉬워졌죠? ^^

별다른 계산 없이 전압분배법칙에 의해 \mathrm{V_{x}}는 6V 라는 것을 알 수 있습니다.

 

아까 제가 부하를 연결하기 전의 테브난 등가회로 양 끝단에는 \mathrm{V_{TH}=V_o} (9V) 전압이 그대로 걸린다고 했는데 기억하시나요?

끊어진 회로에는 전류가 흐르지 않기 때문에 테브난 등가저항 3kΩ을 지나도 전압강하가 일어나지 않았습니다.

하지만 지금은 어떤가요?

이어진 회로에 전류가 흐르면서 테브난 등가저항 3kΩ을 지날 때 3V의 전압강하가 일어납니다.

즉, \mathrm{V_{TH}=V_o \neq V_x} 입니다.

회로의 개방 전압 \mathrm{V_{o}}와 최종적으로 부하에 걸리는 전압 \mathrm{V_{x}}가 다른 이유, 이제는 아시겠죠? ^^

 

 

마치며…

 

이걸로 길고 긴 테브난, 노턴 등가회로 강의가 끝났습니다.

강의에서 노턴 등가회로에 대한 내용을 자세히 다루지는 않았지만 과정 자체는 테브난 등가회로와 비슷하니 인터넷을 조금만 훑어봐도 쉽게 이해하실 수 있을 겁니다.

물론 테브난, 노턴 등가회로 사이의 관계를 이용하셔도 되구요. ㅎㅎ

쉽지도 않고 짧지도 않은 내용이었을텐데 여기까지 따라오시느라 정말로 고생 많으셨습니다.

부족한 글 읽어주셔서 감사드리고, 다음 시간에 더 좋은 글로 찾아뵙겠습니다.

지금까지 공대생의 오아시스였습니다. ^^